Matrices especiales

Matriz Identidad:

La Matriz Identidad es una matriz cuadrada tal que cada uno de sus elementos es igual a cero, salvo los elementos de su diagonal que son todos iguales a uno, se denota con . Formalmente decimos que  para todo  y  para todo .

Las siguientes matrices son matrices identidad del tamaño correspondiente:

Matriz Diagonal:

Una matriz cuadrada es Matriz Diagonal si cada uno de sus elementos fuera de la diagonal es igual a cero, en ocasiones se denotan con . Formalmente decimos que  para todo .

Las siguientes matrices son matrices diagonales del tamaño correspondiente:

Matriz Triangular Superior:

Una matriz cuadrada es una Matriz Triangular Superior si todos los elementos que están por debajo de la diagonal, son iguales a cero, en ocasiones se denotan con 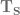. Formalmente decimos que  si .

Las siguientes matrices son matrices triangulares superiores del tamaño correspondiente:

Matriz Triangular inferior:

Una matriz cuadrada es una Matriz Triangular Inferior si todos los elementos que están por encima de la diagonal, son iguales a cero, en ocasiones se denotan con . Formalmente decimos que  si .

Las siguientes matrices son matrices triangulares inferiores del tamaño correspondiente:

Matriz transpuesta:

La matriz transpuesta de una matriz A de dimensión mxn es una matriz de dimensión nxm que tiene por columnas a las filas de A, se denota como AT o A´ si la matriz es real

La siguiente matriz es una matriz transpuesta:

Matriz simétrica:

Una matriz es simétrica si es igual a su transpuesta, es decir A = AT, Como consecuencia de la definición la matriz A debe ser cuadrada.

La siguiente matriz es una matriz simétrica:

Matriz aumentada:

La matriz aumentada o matriz ampliada se forma al añadir una matriz cuadrada a otra matriz. La matriz aumentada se emplea para encontrar la matriz inversa o en la solución de sistemas de ecuaciones lineales.

La siguiente matriz es una matriz aumentada a partir de la matriz A aumentada con la matiz B:

$I_{}$